Volume 11, Issue 2 (Spring 2022)
J Occup Health Epidemiol 2022, 11(2): 91-98 |
Back to browse issues page
Download citation:
BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:



BibTeX | RIS | EndNote | Medlars | ProCite | Reference Manager | RefWorks
Send citation to:
Attanayake A. Vaccination Coverage for COVID-19 in Sri Lanka: With and Without Age Stratification on Susceptible-Infectious-Recovered Simulation. J Occup Health Epidemiol 2022; 11 (2) :91-98
URL: http://johe.rums.ac.ir/article-1-506-en.html
URL: http://johe.rums.ac.ir/article-1-506-en.html
Related article in
Google Scholar
Google Scholar
Similar articles
Senior Lecturer in Statistics, Dept. of Statistics & Computer Science, Faculty of Science, University of Kelaniya, Kelaniya, Sri Lanka. , succ@kln.ac.lk
Article history


Received: 2021/12/3
Accepted: 2022/05/23
ePublished: 2022/06/22
Accepted: 2022/05/23
ePublished: 2022/06/22
Subject:
Epidemiology
Keywords: COVID-19 [MeSH], COVID-19 Vaccines [MeSH], Computer Simulation [MeSH], Epidemiological Models [MeSH]
Full-Text [PDF 524 kb]
(723 Downloads)
| Abstract (HTML) (2113 Views)
Table 1. Total number of cases and deaths in each continent [1]
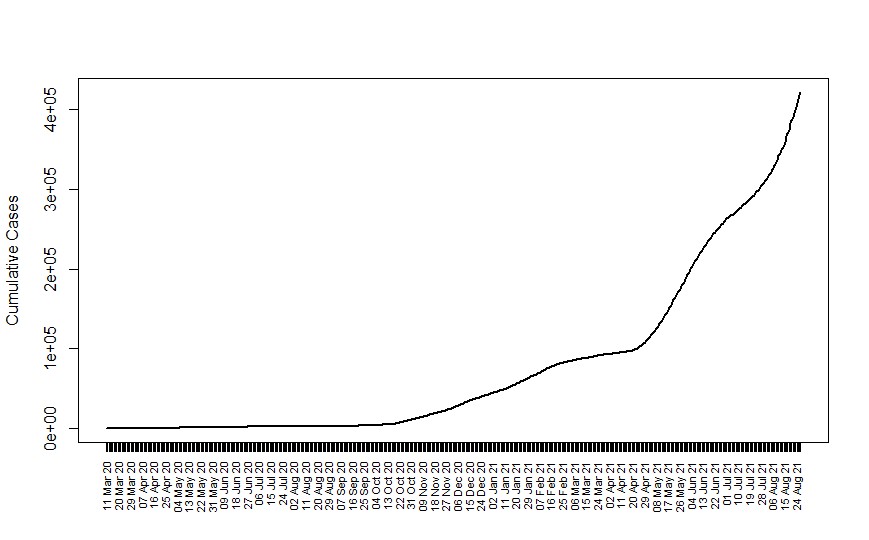
Fig. 1. Cumulative COVID-19 cases in Sri Lanka [12]
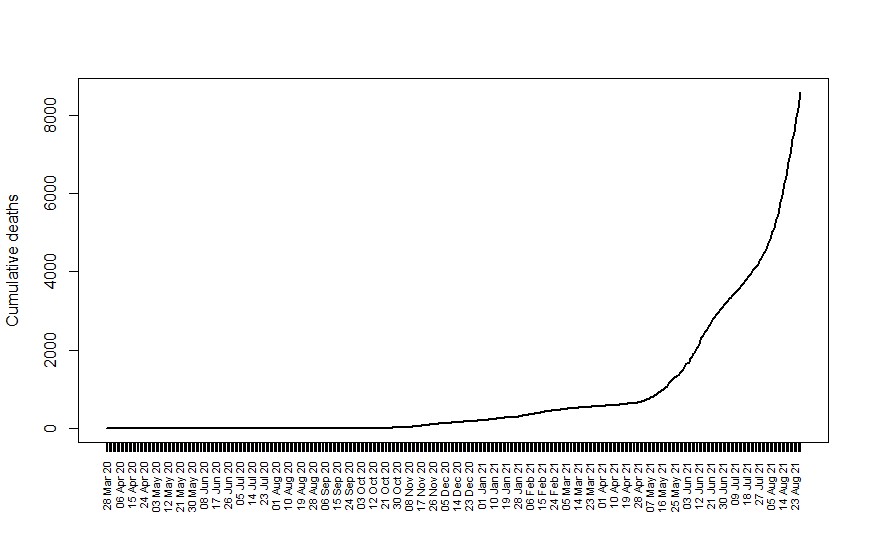
Fig. 2. Cumulative COVID-19 deaths in Sri Lanka [12]
Table 2. Compartments used in the age-stratified SIR model
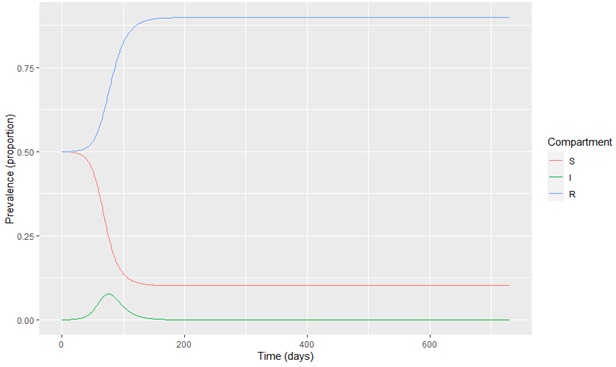
Fig. 3. Model output at 50% vaccination coverage
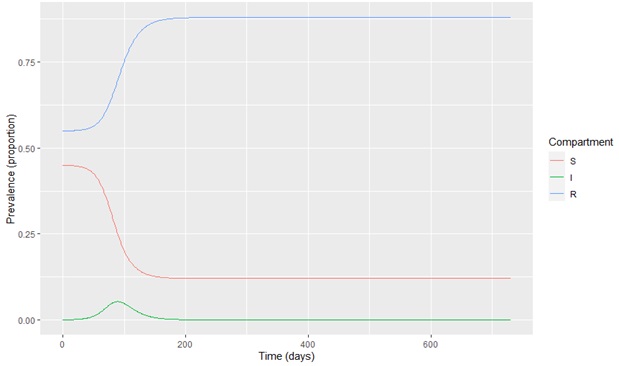
Fig. 4. Model output at 55% vaccination coverage

Fig. 5. Model output at 60% vaccination coverage
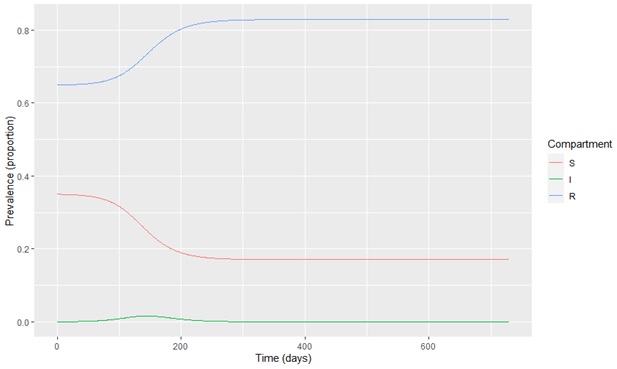
Fig. 6. Model output at 65% vaccination coverage

Fig. 7. Model output at 70% vaccination coverage

Fig. 8. Model output at 75% vaccination coverage

Fig. 9. Model output at p1= 0, p2 = p3 = 0.75

Fig. 10. Model output at p1=0.50, p2 = p3 = 0.75

Fig. 11. Model output at p1= p2 = p3= 0.75

Fig. 12. Model output at p1= p2 = p3 = 0.80
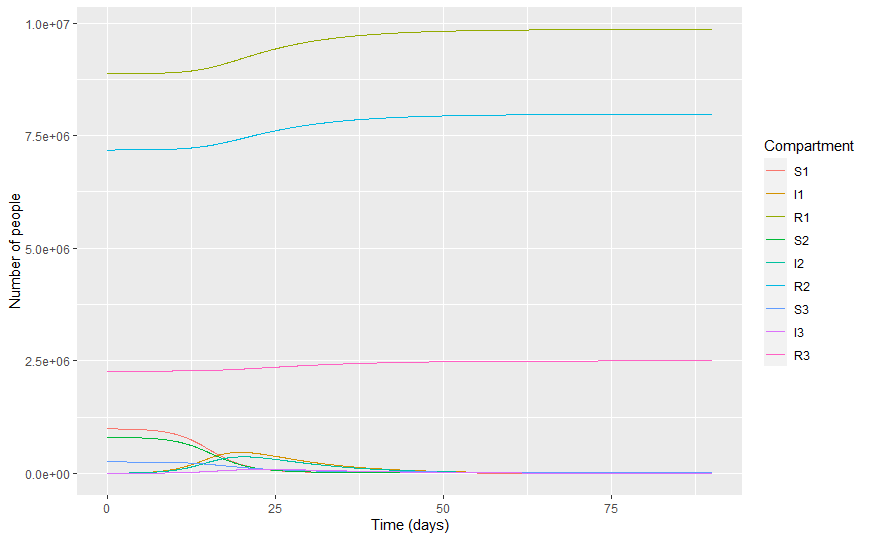
Table 3. Infectious individuals at different levels
Full-Text: (213 Views)
Introduction
COVID-19 is one of the fastest spreading diseases around the world. It was initiated in China in December 2019. The number of COVID-19-affected countries and territories is more than 220 [1]. Maintaining a distance between people, wearing a mask, washing hands frequently, choosing open ventilated places, and following instructions of health professionals are widely recommended and performed preventive measures for the disease [2]. Age and sex are factors that affect the severity and infection of COVID-19 [3]. Some people, medical staff and public transport drivers, face high risks of COVID-19 infections [4]. The survival time of coronavirus differs on different surfaces, increasing the spread of the disease [5, 6, 7]. The airborne transmission may affect the spread of COVID-19 [8]. The attention of the public domain on preventive strategies for the disease should be increased [9].
504,829,432 COVID-19 infected cases and 6,223,540 COVID-19 deaths were reported worldwide as of April 18, 2022 [1]. The USA, India, and Brazil are the top three countries on the list of the total number of COVID-19 infections and the total COVID-19 deaths [1]. Table 1 shows the total number of cases and deaths recorded from the disease as of April 18, 2022, in each continent. As can be seen, the least number of deaths has occurred in Oceania whereas most have occurred in Europe [1]. These figures illustrate the severity of the disease spread in the universe.
COVID-19 is one of the fastest spreading diseases around the world. It was initiated in China in December 2019. The number of COVID-19-affected countries and territories is more than 220 [1]. Maintaining a distance between people, wearing a mask, washing hands frequently, choosing open ventilated places, and following instructions of health professionals are widely recommended and performed preventive measures for the disease [2]. Age and sex are factors that affect the severity and infection of COVID-19 [3]. Some people, medical staff and public transport drivers, face high risks of COVID-19 infections [4]. The survival time of coronavirus differs on different surfaces, increasing the spread of the disease [5, 6, 7]. The airborne transmission may affect the spread of COVID-19 [8]. The attention of the public domain on preventive strategies for the disease should be increased [9].
504,829,432 COVID-19 infected cases and 6,223,540 COVID-19 deaths were reported worldwide as of April 18, 2022 [1]. The USA, India, and Brazil are the top three countries on the list of the total number of COVID-19 infections and the total COVID-19 deaths [1]. Table 1 shows the total number of cases and deaths recorded from the disease as of April 18, 2022, in each continent. As can be seen, the least number of deaths has occurred in Oceania whereas most have occurred in Europe [1]. These figures illustrate the severity of the disease spread in the universe.
Table 1. Total number of cases and deaths in each continent [1]
| Continent | Total number of cases | Total number of deaths |
| Asia | 145,740,356 | 1,416,179 |
| South America | 56,547,763 | 1,291,992 |
| Africa | 11,824,589 | 253,389 |
| Oceania | 6,537,104 | 10,017 |
| North America | 97,395,561 | 1,452,878 |
| Europe | 186,783,338 | 1,799,070 |
To control the disease, many countries have started vaccinating against COVID-19. Nearly 33.4% of the world population has received at least one dose of a COVID-19 vaccine [10]. Until the entire population is vaccinated, individual and social preventive measures can help minimize the COVID-19 spread [11].
The first local COVID-19 case was found in Sri Lanka on March 11, 2020 [1]. As of December 31,
2020, 43,299 COVID-19 infected cases and 204 COVID-19 deaths were reported in Sri Lanka. The country reported 662,827 infections on April 18, 2022, with 16,495 deaths [1]. The distributions of the cumulative number of cases and deaths are depicted in Figures 1 and 2 [12]. According to the figures, further transmissions can be expected in Sri Lanka.
The first local COVID-19 case was found in Sri Lanka on March 11, 2020 [1]. As of December 31,
2020, 43,299 COVID-19 infected cases and 204 COVID-19 deaths were reported in Sri Lanka. The country reported 662,827 infections on April 18, 2022, with 16,495 deaths [1]. The distributions of the cumulative number of cases and deaths are depicted in Figures 1 and 2 [12]. According to the figures, further transmissions can be expected in Sri Lanka.

Fig. 1. Cumulative COVID-19 cases in Sri Lanka [12]

Fig. 2. Cumulative COVID-19 deaths in Sri Lanka [12]
At present (29/08/2021), major social gatherings are banned, and schools are closed in the country. Further, a nationwide lockdown is implemented to control the disease spread. The Delta variant of COVID-19 is spreading at an alarming rate in Sri Lanka, causing many deaths and infections. Currently, the Sri Lankan government is driving the vaccination process as a strategy to deal with the COVID-19. Although Sri Lanka has approved many vaccines, such as Moderna, Pfizer, AstraZeneca, Sinopharm, and Sputnik V, the majority of the population has been vaccinated with Sinopharm. 56.4% of the total population of the country has received at least one dose of the vaccine as of August 28, 2021 [10]. The vaccination process started by classifying the population into age groups. Three age groups are below 30, between 30 – 59, and over 60. However, Sri Lanka has not officially started vaccines among the age group below 30 and is willing to start to control the spread. Research findings show that COVID-19 vaccinations cause non-specific axillary Lymphadenopathy (LA) with increased PET tracer activity [13]. People are usually relucted to be vaccinated against COVID-19 due to assumed side effects and severe reactions, as well as not trusting the protection from the vaccination [14].
Sri Lanka considers vaccinations as its primary controlling strategy against COVID-19. Knowing how much of the population should be vaccinated is essential to mitigate the spread of disease. Additionally, what proportion of children, adults, and elderly populations should be vaccinated is a leading question in the country. Further, knowledge of how many infections will occur in each age group over future months is vital in managing and planning health-related resources. Mathematical models can be utilized in answering these questions. Primarily, Susceptible-Infectious-Recovered (SIR) compartment modeling, one of the cornerstones in mathematical modeling, can provide useful insights into the progression of the disease in various compartments. The SIR modeling has been widely used in COVID-19 in many studies [15, 16, 17, 18]. Some have used the basic SIR model, and some have used its extended versions. Haidere et al., in 2021, discussed important questions that should be considered in developing COVID-19 vaccines [19]. A SIR model development with factors such as vaccination, treatment, and obedience in fuzzy representation can be found in Muhammad et al. (2021) [20]. Wickramaarachchi et al. (2020) presented a modified SEIR model by dividing the infected population into two classes. Their simulation was based on the Sri Lankan context [21]. Research findings by coupling the SIR compartment modeling with vaccination in the Sri Lankan context are rather limited in the literature.
This study aims to adopt a SIR model to describe the vaccination coverage required to erase the spread of COVID-19 in Sri Lanka. Primarily, the study addresses answers to the following questions:
How much of the entire population should be vaccinated to interrupt the COVID-19 spread?
What proportion of children, adults, and elderly populations should be vaccinated to control the COVID-19?
How many infections will occur in each age group over three months period under different vaccine coverages?
The simulations are done for the country. This is significant because Sri Lanka considers vaccinations its major controlling strategy against the COVID-19. Therefore, it is essential to know how much of the population should be vaccinated to mitigate the disease spread. Research findings by coupling the SIR compartment modeling with vaccination in the Sri Lankan context are rather limited in the literature. A basic SIR model addressed the first question with vaccination coverage and without an age stratification. Then, the SIR model compartments were decomposed into age groups to capture the nature of the COVID-19 spread within each. One unique feature of the developed model is that it is based on a simple SIR model and is easy to understand and simulate.
Materials and Methods
The present research was a longitudinal study based on the Sri Lankan context. No samples were used; hence, no sampling method was considered. Data on the age distribution of the population were acquired from the census report of the Census and Statistics Center in Sri Lanka, consisting of the population in each age group (below 30, between 30-59, and over 60) [22]. This was a mathematical modeling study in which the population (people) in Sri Lanka were divided into susceptible to COVID-19, Infected with COVID-19, and Recovered from COVID-19. Then, solving differential equations, the progress of three compartments (susceptible, infected, and recovered) with various vaccination coverages were investigated to determine the required vaccination coverage to interrupt the COVID-19 spread. Age-stratified and unstratified SIR models were adopted to describe the vaccination coverage for COVID-19 in the country. R programming language [23] packages of 'dissolve,' 'reshape2,' and 'ggplot2' were basically utilized in the analysis.
The SIR (Susceptible-Infectious-Recovered) Model: The SIR model is the basic form of compartment modeling [24]. This modeling strategy enables the description of disease spread using three Susceptible, Infected and Recovered compartments. The Susceptible denoted by 'S' refers to those susceptible but not currently infected with the disease. The Infected denoted by 'I' refers to those infected. The Recovered represented by 'R' shows those who recovered from the disease and have immune. A system of three differential equations of the SIR model can be represented as follows:
Formula 1.



This model assumes a fixed population size of N, where . S(t), I(t), and R(t) denote the number of individuals in the three groups as functions of time t. The dynamics of the model are measured by the parameters β and γ [25], representing the rates of transmission from S to I and I to R, respectively.
In this study, this model was applied to COVID-19 disease. It was modified to capture the percentage
of vaccine coverage in the population (p) and then (1 – p) of the population that is only susceptible to the disease. The constant infection rate (β) was assumed as 0.4 and the recovery rate (γ) as 0.1. In order to address the second and third questions of the study, S, I, and R compartments were further decomposed as S1, S2, S3, I1, I2, I3, R1, R2, and R3 to represent children, adults, and elderly populations in each of the three compartments (Table 2). The percentage of vaccine coverage in the population of <30 age group was denoted as p1. Also, p2 and p3 denoted the percentage of vaccine coverage in the population group between 30 -59 and over 60, respectively. Therefore, the variables in the study compromised compartments S1, S2, S3, I1, I2, I3, R1, R2, & R3, infection rate (β), recovery rate (γ), and p1, p2, & p3. This study assumed the people who recovered from the COVID-19 to be fully immune. In reality, this assumption may not be valid, and investigations are still in progress in this regard [26].
Sri Lanka considers vaccinations as its primary controlling strategy against COVID-19. Knowing how much of the population should be vaccinated is essential to mitigate the spread of disease. Additionally, what proportion of children, adults, and elderly populations should be vaccinated is a leading question in the country. Further, knowledge of how many infections will occur in each age group over future months is vital in managing and planning health-related resources. Mathematical models can be utilized in answering these questions. Primarily, Susceptible-Infectious-Recovered (SIR) compartment modeling, one of the cornerstones in mathematical modeling, can provide useful insights into the progression of the disease in various compartments. The SIR modeling has been widely used in COVID-19 in many studies [15, 16, 17, 18]. Some have used the basic SIR model, and some have used its extended versions. Haidere et al., in 2021, discussed important questions that should be considered in developing COVID-19 vaccines [19]. A SIR model development with factors such as vaccination, treatment, and obedience in fuzzy representation can be found in Muhammad et al. (2021) [20]. Wickramaarachchi et al. (2020) presented a modified SEIR model by dividing the infected population into two classes. Their simulation was based on the Sri Lankan context [21]. Research findings by coupling the SIR compartment modeling with vaccination in the Sri Lankan context are rather limited in the literature.
This study aims to adopt a SIR model to describe the vaccination coverage required to erase the spread of COVID-19 in Sri Lanka. Primarily, the study addresses answers to the following questions:
How much of the entire population should be vaccinated to interrupt the COVID-19 spread?
What proportion of children, adults, and elderly populations should be vaccinated to control the COVID-19?
How many infections will occur in each age group over three months period under different vaccine coverages?
The simulations are done for the country. This is significant because Sri Lanka considers vaccinations its major controlling strategy against the COVID-19. Therefore, it is essential to know how much of the population should be vaccinated to mitigate the disease spread. Research findings by coupling the SIR compartment modeling with vaccination in the Sri Lankan context are rather limited in the literature. A basic SIR model addressed the first question with vaccination coverage and without an age stratification. Then, the SIR model compartments were decomposed into age groups to capture the nature of the COVID-19 spread within each. One unique feature of the developed model is that it is based on a simple SIR model and is easy to understand and simulate.
Materials and Methods
The present research was a longitudinal study based on the Sri Lankan context. No samples were used; hence, no sampling method was considered. Data on the age distribution of the population were acquired from the census report of the Census and Statistics Center in Sri Lanka, consisting of the population in each age group (below 30, between 30-59, and over 60) [22]. This was a mathematical modeling study in which the population (people) in Sri Lanka were divided into susceptible to COVID-19, Infected with COVID-19, and Recovered from COVID-19. Then, solving differential equations, the progress of three compartments (susceptible, infected, and recovered) with various vaccination coverages were investigated to determine the required vaccination coverage to interrupt the COVID-19 spread. Age-stratified and unstratified SIR models were adopted to describe the vaccination coverage for COVID-19 in the country. R programming language [23] packages of 'dissolve,' 'reshape2,' and 'ggplot2' were basically utilized in the analysis.
The SIR (Susceptible-Infectious-Recovered) Model: The SIR model is the basic form of compartment modeling [24]. This modeling strategy enables the description of disease spread using three Susceptible, Infected and Recovered compartments. The Susceptible denoted by 'S' refers to those susceptible but not currently infected with the disease. The Infected denoted by 'I' refers to those infected. The Recovered represented by 'R' shows those who recovered from the disease and have immune. A system of three differential equations of the SIR model can be represented as follows:
Formula 1.



This model assumes a fixed population size of N, where . S(t), I(t), and R(t) denote the number of individuals in the three groups as functions of time t. The dynamics of the model are measured by the parameters β and γ [25], representing the rates of transmission from S to I and I to R, respectively.
In this study, this model was applied to COVID-19 disease. It was modified to capture the percentage
of vaccine coverage in the population (p) and then (1 – p) of the population that is only susceptible to the disease. The constant infection rate (β) was assumed as 0.4 and the recovery rate (γ) as 0.1. In order to address the second and third questions of the study, S, I, and R compartments were further decomposed as S1, S2, S3, I1, I2, I3, R1, R2, and R3 to represent children, adults, and elderly populations in each of the three compartments (Table 2). The percentage of vaccine coverage in the population of <30 age group was denoted as p1. Also, p2 and p3 denoted the percentage of vaccine coverage in the population group between 30 -59 and over 60, respectively. Therefore, the variables in the study compromised compartments S1, S2, S3, I1, I2, I3, R1, R2, & R3, infection rate (β), recovery rate (γ), and p1, p2, & p3. This study assumed the people who recovered from the COVID-19 to be fully immune. In reality, this assumption may not be valid, and investigations are still in progress in this regard [26].
Table 2. Compartments used in the age-stratified SIR model
| Compartment | Definition |
| S1 | Susceptible in <30 years of age |
| I1 | Infected in <30 years of age |
| R1 | Recovered in <30 years of age |
| S2 | Susceptible in 30-59 years of age |
| I2 | Infected in 30-59 years of age |
| R3 | Recovered in 30-59 years of age |
| S3 | Susceptible in 60 ≥ years of age |
| I3 | Infected in 60 ≥ years of age |
| R3 | Recovered in 60 ≥ years of age |
Results
The simulation results of the SIR model without age stratification are shown in Figures 3 to 8. The x-axis denotes the number of days, and the y-axis denotes the prevalence proportion in each compartment. Figure 3 shows the distribution of susceptible, infected, and recovered compartments due to COVID-19 at 50% of vaccination coverage in the country. Further, Figure 4 shows the distribution of susceptible, infected, and recovered compartments due to COVID-19 at 55% of vaccination coverage in the country. The infected population can be seen in Figures 3 and 4 with 50% and 55% vaccination coverage. Figures 5 to 8 illustrate simulations at various percentages of vaccination coverages (p) in the population.
The simulation results of the SIR model without age stratification are shown in Figures 3 to 8. The x-axis denotes the number of days, and the y-axis denotes the prevalence proportion in each compartment. Figure 3 shows the distribution of susceptible, infected, and recovered compartments due to COVID-19 at 50% of vaccination coverage in the country. Further, Figure 4 shows the distribution of susceptible, infected, and recovered compartments due to COVID-19 at 55% of vaccination coverage in the country. The infected population can be seen in Figures 3 and 4 with 50% and 55% vaccination coverage. Figures 5 to 8 illustrate simulations at various percentages of vaccination coverages (p) in the population.

Fig. 3. Model output at 50% vaccination coverage

Fig. 4. Model output at 55% vaccination coverage

Fig. 5. Model output at 60% vaccination coverage

Fig. 6. Model output at 65% vaccination coverage

Fig. 7. Model output at 70% vaccination coverage

Fig. 8. Model output at 75% vaccination coverage
As seen in the figures, the transmission of COVID-19 can be destroyed entirely in Sri Lanka at 75% of the vaccine coverage in the entire population. This model assumes that an individual has complete immunity to the COVID-19 after vaccination.
An age-stratified SIR model is used to find the proportion of children, adults, and elderly populations that should be vaccinated to control the COVID-19 transmission. The number of people in the <30 age group is 9,861,646 (N1). The number of people in the 30-59 age group is 7,977,219 (N2), whereas, in the 60 ≥ age group, it is 2,520,573 (N3) [22]. p1, p2, and p3 denote vaccination coverages in children, adults, and the elderly. The model is run for three months period. Simulation results of the age-stratified SIR model at various vaccine coverages are depicted in Figures 9 to 13.
Figure 9 shows the distribution of susceptible, infected, and recovered compartments at 75% of vaccination coverage in the 30-59 and over 60 age groups. According to this figure, further transmissions are possible in that vaccination coverage. The infected population in each age group can be seen in Figure 9 with the vaccination coverage.
An age-stratified SIR model is used to find the proportion of children, adults, and elderly populations that should be vaccinated to control the COVID-19 transmission. The number of people in the <30 age group is 9,861,646 (N1). The number of people in the 30-59 age group is 7,977,219 (N2), whereas, in the 60 ≥ age group, it is 2,520,573 (N3) [22]. p1, p2, and p3 denote vaccination coverages in children, adults, and the elderly. The model is run for three months period. Simulation results of the age-stratified SIR model at various vaccine coverages are depicted in Figures 9 to 13.
Figure 9 shows the distribution of susceptible, infected, and recovered compartments at 75% of vaccination coverage in the 30-59 and over 60 age groups. According to this figure, further transmissions are possible in that vaccination coverage. The infected population in each age group can be seen in Figure 9 with the vaccination coverage.

Fig. 9. Model output at p1= 0, p2 = p3 = 0.75

Fig. 10. Model output at p1=0.50, p2 = p3 = 0.75

Fig. 11. Model output at p1= p2 = p3= 0.75

Fig. 12. Model output at p1= p2 = p3 = 0.80

Fig.13. Model output at p1= p2 = p3 = 0.90
Figures 10 to 1.3 show the distribution of susceptible, infected, and recovered compartments in each age group at different vaccination levels. Model outputs show that over 90% of vaccination coverage in each age group is required to interrupt the COVID-19 transmission in Sri Lanka.
Some useful findings in the model outputs in Figures 9 to 13 are summarized in Table 3. The expected peak point (maximum point) in each model at each age group is summarized in Table 3. The expected number of COVID-19 patients at the peak point is further presented in Table 3. The last row of Table 3 shows that with the vaccination coverage of 75% in the over 60 age group, the maximum number of patients can be expected on the 10th day, as 381316 cases.
Some useful findings in the model outputs in Figures 9 to 13 are summarized in Table 3. The expected peak point (maximum point) in each model at each age group is summarized in Table 3. The expected number of COVID-19 patients at the peak point is further presented in Table 3. The last row of Table 3 shows that with the vaccination coverage of 75% in the over 60 age group, the maximum number of patients can be expected on the 10th day, as 381316 cases.
Table 3. Infectious individuals at different levels
| Vaccine coverage | Age group | Peak point (day) | Infectious individuals at the peak point |
| p1 = 0 p2 = 0.75 p3 = 0.75 |
<30 30 – 59 60 ≥ |
3 4 6 |
8467175 1600397 448319 |
| p1 = 0.50 p2 = 0.75 p3 = 0.75 |
<30 30 – 59 60 ≥ |
6 7 8 |
3874721 1492283 409683 |
| p1 = 0.75 p2 = 0.75 p3 = 0.75 |
<30 30 – 59 60 ≥ |
8 9 10 |
1762237 1406515 381316 |
| p1 = 0.80 p2 = 0.80 p3 = 0.80 |
<30 30 – 59 60 ≥ |
10 10 13 |
1313415 1045649 276229 |
| p1 = 0.90 p2 = 0.90 p3 = 0.90 |
<30 30 – 59 60 ≥ |
19 20 23 |
465138 365838 86551 |
Clearly, the peak point of the epidemic shifts with the increase in the vaccination coverage in each age group. Further, the number of infections in each age group reduces with the increase in vaccination coverage.
Discussion
This study aims to implement a SIR model to describe the vaccination coverage required to erase the transmission of COVID-19 in Sri Lanka. Age-stratified and unstratified SIR models with vaccination coverage were utilized for this purpose. The following questions were addressed in the study:
Discussion
This study aims to implement a SIR model to describe the vaccination coverage required to erase the transmission of COVID-19 in Sri Lanka. Age-stratified and unstratified SIR models with vaccination coverage were utilized for this purpose. The following questions were addressed in the study:
- How much of the entire population should be vaccinated to interrupt the spread of the COVID-19?
- What proportion of children, adults, and elderly populations should be vaccinated to control the COVID-19?
- How many infections will occur in each age group over three months under different vaccine coverages?
Based on the age-unstratified SIR model, 75% vaccination coverage is required in the entire population to completely interrupt the disease spread. The age-stratified SIR model shows that over 90% of vaccination coverage in each age group is required to completely interrupt the disease transmission in Sri Lanka. The number of infections in each age group reduces with the increase in vaccination coverage.
The knowledge of vaccination coverage and infectiousness in COVID-19 can provide tremendous advantages in Sri Lanka, including implementing and enhancing controlling actions, handling the process cost-effectively, discovering more opportunities and possibilities to manage the epidemic, determining the required number of vaccine doses, calculating the cost associated with vaccination, and properly managing health-related resources. A country should have a proper vaccination strategy to succeed in this process. Therefore, the findings of this study can direct possible actions to be implemented in planning the vaccination process, thus mitigating the COVID-19 impact.
The developed SIR models in this study assume that people who recover from the COVID-19 are entirely immune to the disease. Further, it is assumed that full immunity to the COVID-19 will be developed in the body after the vaccination. This assumption may not hold in the real scenario as various complicated variants of the virus are evolving, which may not respond to the vaccinations formulated so far. Additionally, the model assumes homogeneous and well-mixed populations. These assumptions are the study's limitations and may control the productivity and throughput of the modeling process used. Further, this study has not analyzed doses and types of vaccination separately.
Studies related to COVID-19 vaccination coverage in the Sri Lankan context are limited in the literature. Kraft et al. (2021) [27] investigated the COVID-19 vaccination coverage in Norway. They similarly found that the high vaccination coverages limited the COVID-19 infection, hospitalization, and deaths. This study further confirmed that the number of COVID-19 infections in each age group of Sri Lanka was reduced with increased vaccination coverage. SIR simulations of the COVID-19 pandemic in Ukraine [28] and Cameroon [29] showed some reliable estimations and predictions. Thus, the application of the SIR simulation on COVID-19 can be justified. The population needed to be vaccinated against COVID-19 over four states in India (Rajasthan, Maharashtra, Gujarat, and Delhi) was investigated in a study through the SIR simulation [30]. This and similar studies on required vaccination coverage are useful because it is costly and unnecessary to vaccinate the entire population in a country.
This study applied compartment modeling to find the required vaccination coverage to interrupt the COVID-19 transmission. Other than compartment modeling, agent-based modeling and clustering mechanisms can be suggested to find the answers to the research questions.
Conclusion
The number of COVID-19 infections in age groups below 30, between 30-59, and over 60 is reduced with increased vaccination coverage for the disease in Sri Lanka. 75% vaccination coverage is required in the entire population, and over 90% of vaccination coverage in each age group (below 30, between 30-59, and over 60) is required to interrupt the COVID-19 transmission completel. Therefore, authorities should expand the percentages of COVID-19 vaccinations in the country.
Acknowledgement
The author would like to thank the Department of Census and Statistics, Sri Lanka, for providing data for this research.
Conflict of interest: None declared.
The knowledge of vaccination coverage and infectiousness in COVID-19 can provide tremendous advantages in Sri Lanka, including implementing and enhancing controlling actions, handling the process cost-effectively, discovering more opportunities and possibilities to manage the epidemic, determining the required number of vaccine doses, calculating the cost associated with vaccination, and properly managing health-related resources. A country should have a proper vaccination strategy to succeed in this process. Therefore, the findings of this study can direct possible actions to be implemented in planning the vaccination process, thus mitigating the COVID-19 impact.
The developed SIR models in this study assume that people who recover from the COVID-19 are entirely immune to the disease. Further, it is assumed that full immunity to the COVID-19 will be developed in the body after the vaccination. This assumption may not hold in the real scenario as various complicated variants of the virus are evolving, which may not respond to the vaccinations formulated so far. Additionally, the model assumes homogeneous and well-mixed populations. These assumptions are the study's limitations and may control the productivity and throughput of the modeling process used. Further, this study has not analyzed doses and types of vaccination separately.
Studies related to COVID-19 vaccination coverage in the Sri Lankan context are limited in the literature. Kraft et al. (2021) [27] investigated the COVID-19 vaccination coverage in Norway. They similarly found that the high vaccination coverages limited the COVID-19 infection, hospitalization, and deaths. This study further confirmed that the number of COVID-19 infections in each age group of Sri Lanka was reduced with increased vaccination coverage. SIR simulations of the COVID-19 pandemic in Ukraine [28] and Cameroon [29] showed some reliable estimations and predictions. Thus, the application of the SIR simulation on COVID-19 can be justified. The population needed to be vaccinated against COVID-19 over four states in India (Rajasthan, Maharashtra, Gujarat, and Delhi) was investigated in a study through the SIR simulation [30]. This and similar studies on required vaccination coverage are useful because it is costly and unnecessary to vaccinate the entire population in a country.
This study applied compartment modeling to find the required vaccination coverage to interrupt the COVID-19 transmission. Other than compartment modeling, agent-based modeling and clustering mechanisms can be suggested to find the answers to the research questions.
Conclusion
The number of COVID-19 infections in age groups below 30, between 30-59, and over 60 is reduced with increased vaccination coverage for the disease in Sri Lanka. 75% vaccination coverage is required in the entire population, and over 90% of vaccination coverage in each age group (below 30, between 30-59, and over 60) is required to interrupt the COVID-19 transmission completel. Therefore, authorities should expand the percentages of COVID-19 vaccinations in the country.
Acknowledgement
The author would like to thank the Department of Census and Statistics, Sri Lanka, for providing data for this research.
Conflict of interest: None declared.
References
1. Worldometer, COVID-19 Coronaviru andemic, [Internet]. 2022 Apr 18. Available from: https://www.worldometers.info/coronavirus/ [Report]
2. Barber SJ, Kim H. COVID-19 Worries and Behavior Changes in Older and Younger Men and Women. J Gerontol B Psychol Sci Soc Sci. 2021;76(2):e17-23. [DOI] [PMID] [PMCID]
3. [3] Ritchie H, Mathieu E, Rodés-Guirao L, Appel C, Giattino C, Ortiz-Ospina E, et al. Coronavirus Pandemic (COVID-19) Vaccinations. World Data. 2021. [Report]
4. 4. Humanitarian Data Exchange. Novel Coronavirus (COVID-19) Cases Data. [Internet]. 2021 Aug 27. Available from: https://data.humdata.org/event/covid-19. [Report]
5. Agarwal P, Jhajharia K. Data analysis and modeling of COVID-19. J Stat Manage Syst. 2021;24(1):1-16. [DOI]
6. Alharbi Y, Alqahtani A, Albalawi O, Bakouri M. Epidemiological Modeling of COVID-19 in Saudi Arabia: Spread Projection, Awareness, and Impact of Treatment. Appl Sci. 2020;10(17):5895. [DOI]
7. Liu M, Thomadsen R, Yao S. Forecasting the spread of COVID-19 under different reopening strategies. Sci Rep. 2020;10(1):20367. [DOI] [PMID] [PMCID]
8. Yadav RSYRS. Mathematical Modeling and Simulation of SIR Model for COVID-2019 Epidemic Outbreak: A Case Study of India. INFOCOMP J Comput Sci. 2020;19(2):01-09. [DOI]
9. Haidere MF, Ratan ZA, Nowroz S, Zaman SB, Jung Y, Hosseinzadeh H, Cho JY. COVID-19 Vaccine: Critical Questions with Complicated Answers. Biomol Ther (Seoul). 2021;29(1):1-10. [DOI] [PMID] [PMCID]
10. Abdy M, Side S, Annas S, Wahyuddin Nur, Wahidah Sanusi. An SIR epidemic model for COVID-19 spread with fuzzy parameter: the case of Indonesia. Adv Differ Equ. 2021;2021(1):105 [DOI] [PMID] [PMCID]
11. [11] Wickramaarachchi, WPTM, Perera, SSN, Jayasinghe S. COVID-19 Epidemic in Sri Lanka: A Mathematical and Computational Modelling Approach to Control. Comput Math Methods Med. 2020;2020:4045064 [DOI] [PMID] [PMCID]
12. Population Tables. Census of Population and Housing – 2012 Sri Lanka. 14th ed. Battaramulla, Sri Lanka: Department of Census and Statistics; 2015. [Article]
13. R Core Team. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; 2018. [Report]
14. Kermack WO, McKendrick AG. A Contribution to the Mathematical Theory of Epidemics. Proc Math Phys Eng Sci. 1927;115(772):700-21. [DOI]
15. World Health Organization, 2020. “‘Immunity passports” in the context of COVID-19’. Geneva, Switzerland: World Health Organization; 2021. [DOI]
16. Puspitasari IM, Yusuf L, Sinuraya RK, Abdulah R, Koyama H. Knowledge, Attitude, and Practice During the COVID-19 Pandemic: A Review. J Multidiscip Healthc. 2020;13:727-33. [DOI] [PMID] [PMCID]
17. Udwadia ZF, Raju RS. How to protect the protectors: 10 lessons to learn for doctors fighting the COVID -19 coronavirus. Med J Armed Forces India. 2020;76(2):128-31. [DOI] [PMID] [PMCID]
18. de Gier B, de Oliveira BLP, van Gaalen RD, de Boer PT, Alblas J, Ruijten M, et al. Occupation- and age-associated risk of SARS-CoV-2 test positivity, the Netherlands, June to October 2020. Euro Surveill. 2020;25(50):2001884. [DOI]
19. Razzini K, Castrica M, Menchetti L, Maggi L, Negroni L, Orfeo NV, Pizzoccheri A, Stocco M, Muttini S, Balzaretti CM. SARS-CoV-2 RNA detection in the air and on surfaces in the COVID-19 ward of a hospital in Milan, Italy. Sci Total Environ. 2020;742:140540. [DOI] [PMID] [PMCID]
20. Riddell S, Goldie S, Hill A, Eagles D, Drew TW. The effect of temperature on persistence of SARS-CoV-2 on common surfaces. Virol J. 2020;17(1):145. [DOI] [PMID] [PMCID]
21. Zhou J, Otter JA, Price JR, Cimpeanu C, Garcia DM, Kinross J, Boshier PR, Mason S, Bolt F, Holmes AH, Barclay WS. Investigating Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2) Surface and Air Contamination in an Acute Healthcare Setting During the Peak of the Coronavirus Disease 2019 (COVID-19) Pandemic in London. Clin Infect Dis. 2021;73(7):e1870-7. [DOI] [PubMed] [PMCID]
22. Kraft KB, Godoy AA, Vinjerui KH, Kour P, Kjollesdal MKR, Indseth T. COVID-19 vaccination by immigrant background. Tidsskr Nor Legeforen. 2022;141(2). [DOI] [PMID]
23. Ram K, Thakur RC, Singh DK, Kawamura K, Shimouchi A, Sekine Y, Nishimura H, Singh SK, Pavuluri CM, Singh RS, Tripathi SN. Why airborne transmission hasn't been conclusive in case of COVID-19? An atmospheric science perspective. Sci Total Environ. 2021;773:145525. [DOI] [PMID] [PMCID]
24. Firouzbakht M, Omidvar S, Firouzbakht S, Asadi-Amoli A. COVID-19 preventive behaviors and influencing factors in the Iranian population; a web-based survey. BMC Public Health. 2021;21(1):143. [DOI] [PMID] [PMCID]
25. Ridenhour B, Kowalik JM, Shay DK. Unraveling R0: Considerations for public health applications. Am J Public Health.2018; 108(Suppl 6):S445-54. [DOI] [PMCID]
26. Orevi M, Chicheportiche A, Ben Haim S. Lessons Learned from Post-COVID-19 Vaccination PET/CT Studies. J Nucl Med. 2022;63(3):453-60. [DOI] [PubMed] [PMCID]
27. Kaplan RM, Milstein A. Influence of a COVID-19 vaccine's effectiveness and safety profile on vaccination acceptance. Proc Natl Acad Sci U S A. 2021;118(10):e2021726118. [DOI] [PMID] [PMCID]
28. [28] Saxena R, Jadeja M, Bhateja V. Propagation Analysis of COVID-19: An SIR Model-Based Investigation of the Pandemic. Arab J Sci Eng. 2021;10:1-13. [DOI] [PubMed] [PMCID]
29. [29] Igor N. Detections and SIR simulations of the COVID-19 PANDEMIC WAVES IN Ukraine.Comput Math Biophys. 2021;9(1):46-65. [DOI]
Send email to the article author
| Rights and permissions | |
 |
This work is licensed under a Creative Commons Attribution 4.0 International License. |








